Environnement,y=f(x,y,z,t), Environnement

Le mystère mathématique d’une ancienne tablette babylonienne

Ils démontrent également comment les anciens scribes, qui ont utilisé une base arithmétique numérique similaire à notre horloge plutôt que le système de base de 10, pourraient avoir généré les nombres sur la tablette en utilisant leurs techniques mathématiques.

111,666

666 and the Magickal Seal of the Sun

The “Seals of the Planets,” popular before the time of Christ according to Budge (Amulets and Superstitions), are interesting because the seal containing “the Grand Number of the Sun” contains the very sacred number 36 laid out in a 6×6 square with the numbers from 1 to 36 so arranged that they add up the same in all directions, with the total of the whole seal 666.

Though popular also in Eastern lands, the Greek and Roman, or Latin, inscriptions on these seals show also their popularity in the West.. Since the sun-god was considered as the ruler over the 36 constellations of the sky and the 36 rooms of the circle of the zodiac, it was inevitable that the summary number of the numbers from 1 to 36, the number 666 should have been assigned to the sun as the ruler over all the gods of heaven and earth.

Babylonian astrologers divided the starry heavens into 36 constellations (ten days each). These were represented by different amulets called “Sigilla Solis,” or the Sun Seal. These amulets were worn by the pagan priests and they contained all the numbers from 1 to 36. By these figures they claimed to be able to foretell future events. These amulets were usually made of gold, yellow being the sun color. While being carried, these amulets were wrapped in yellow silk, as it was thought that the bearer would thus receive the beneficent powers believed to emanate from that jewel.

Adding the numbers of any column either horizontally or vertically, and also the two diagonals crossing the square, the total is the same — 111. The sum of the six columns, either horizontally or vertically, is 666. The illustrations below taken from actual amulets in the Berlin Museum.

The 6×6 Magic Square of the Sun contains the first 36 numbers arranged in such a fashion so that each line of numbers, weather added horizontally, vertically or diagonally from corner to corner, will yield the “solar number” 111. The entire magic square therefore equals 666, a number which was significant to early Christian mystics.   In Hebrew Kabbalah, the names of the intelligence of the Sun and Spirit of the Sun were designed to equal 111 and 666 respectively. Like 888, 666 is an important musical number, for .666 is the ration of the perfect fifth, the most powerful harmonic interval.  — From Jesus Christ, Sun of God (Fidler)

http://blog.world-mysteries.com/science/numbers-magick/

Gauss

Carl Friedrich Gauss (1777-1855), 

philosophe et mathématicien Allemand

 surnommé « le prince des mathématiques ».

repeating digits

Interesting, multiples of 3 multiplied by 37 = repeating digits
(1×3) or 1+1+1=3 x 37 = 111
(2×3) or 2+2+2=6 x 37 = 222
(3×3) or 3+3+3=9 x 37 = 333
(4×3) or 4+4+4=12 x 37 = 444
(5×3) or 5+5+5=15 x 37 = 555
(6×3) or 6+6+6=18 x 37 = 666
(7×3) or 7+7+7=21 x 37 = 777
(8×3) or 8+8+8=24 x 37 = 888
(9×3) or 9+9+9=27 x 37 = 999

et 333667*3*x .......

5.5511151231257827021181583404541015625 × 10^-17=1/2^54 etc ....

999 = neuf fois neuf = 999 999 999

Triangle de Pascal et Fibonacci

http://blog.world-mysteries.com/science/numbers-magick/

Triangle de Pascal et Sierpinski

Si on le construit à partir d'un triangle de Pascal avec 2ⁿ lignes et que l'on colore les nombres pairs en blanc et les nombres impairs en noir, alors le résultat est une approximation du triangle de Sierpiński.

http://blog.world-mysteries.com/science/numbers-magick/

Symbolique du nombre 7 (Chiffre)

SEPT

Fonction GAMMA

Lien avec la factorielle[modifier | modifier le code]

De ${\displaystyle \Gamma (z+1)=z\;\Gamma (z)}$ et Γ(1) = 1, on déduit :

${\displaystyle \forall \,n\in \mathbb {N} ,\;\Gamma (n+1)=n!}$.

La fonction gamma est donc généralement perçue comme un prolongement de la factorielle à l'ensemble des nombres complexes (excepté les entiers négatifs ou nuls).
Une notation alternative est la fonction Π, introduite par Gauss :

${\displaystyle \Pi (z)=\Gamma (z+1)=z\;\Gamma (z)}$ (et donc ${\displaystyle \Gamma (z)=\Pi (z-1)=\Pi (z)/z}$),

de telle façon que :

${\displaystyle \Pi (n)=n!}$.

Formule de multiplication[modifier | modifier le code]

La fonction gamma vérifie également la formule de duplication : ${\displaystyle \Gamma (z)\;\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z).}$
La formule de duplication est un cas particulier du théorème de multiplication :
${\displaystyle \Gamma (z)\;\Gamma \left(z+{\frac {1}{m}}\right)\;\Gamma \left(z+{\frac {2}{m}}\right)\cdots \Gamma \left(z+{\frac {m-1}{m}}\right)=(2\pi )^{(m-1)/2}\;m^{1/2-mz}\;\Gamma (mz).}$ Cette fonction apparaît également dans des formules incluant la fonction zêta de Riemann.

Loi de Benford

http://fr.wikipedia.org/wiki/Loi_de_Benford



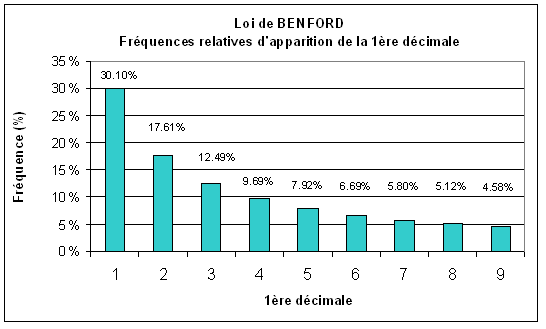
http://www.math-info.univ-paris5.fr/smel/articles/benford/cadre_benford.html

Resources

Calculateur en ligne de la loi de Benford
Fréquences relatives d’apparition de la 1ère décimale d’un résultat de mesure selon la Loi de Benford:

Loi de Benford et suites récurrentes   La loi de Benford prévoit que dans les ensembles de nombres, ( prix des articles contenus dans un caddie, masses moléculaires des produits présentés dans un catalogue, population des agglomérations d'un pays...), le 1er chiffre (celui de gauche ) sera "1" dans 30.1% des cas, "2" dans 17.6% ... et "9" dans seulement 4.6%. Surprenant mais logique : statistiquement vérifiable et mathématiquement démontrable.   Et avec les suites récurrentes ? Si pour la célèbre suite de Fibonacci l'accord est parfait, dans la suite un=4un-1 +3un-2 , avec u0=2 et u1=11, tous les nombres depuis u0 jusqu'à u200 (u200= 5.98..10 133) commencent par 1, 2 ou 5 avec une rigoureuse régularité, mais au-delà ?

pi , une fraction continue

La fraction continue 1²/(6+3²/(6+5²/(6+7²/(6+9²/(6+11²/(6+13²/(6+15²/(6+17²/(etc...))))))))) est exactement égale à la partie décimale de Pi, soit 0,14159265358979... Il suffit donc de lui ajouter 3 pour obtenir la valeur exacte de Pi :

Platon

L'objet des mathématiques et l'objet de la dialectique selon Platon

1/2^n

La série de terme général (1/2)ⁿ est convergente et sa somme vaut : ${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\cdots =2.}$
1/(2^n)
1/2^52 = 2.220446049250313080847263336181640625 × 10^-16
1/(2^54) = 5.5511151231257827021181583404541015625 × 10^-17

Nombre DEMLO

Nombre DEMLO

OEIS

Somme des chiffres
Pour les neuf premiers la somme des chiffres est un carré. En effet, pour n = 5, on a: 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 2 x (1 + 2 + + 4 ) + 5 = 2 x (1 + 2 + … + n-1) + n = 2 x  (n – 1) n / 2 + n =        (n – 1) n + n =         n² Voir Somme des nombres consécutifs La suite des sommes: 1, 4, 9, 16, 25, 36, 49, 64, 81, 82, 85, 90, 97, 106, 117, 130, 145, 162, 163, 166, 171, 178, 187, 198, 211, 226, …

Définition des nombres de Demlo selon Kaprekar
Un nombre de Demlo est composé de trois parties: Ga, Mi et Dr concaténées. D = concat(Ga, Mi, Dr)	Mi est un repdigit en a. Ga et Dr ont le même nombre de chiffres p. (un 0 peut être ajouté à gauche de Ga si nécessaire). Ga + Dr = repdigit en a (comme pour Mi).

Passé , Présent, Avenir  

repunit

The term repunit comes from the words 'repeated' and 'unit;' so repunits are positive integers in which every digit is one. (This term was coined by A. H. Beiler in [Beiler1964].)

 For example, R₁=1, R₂=11, R₃=111, and R_n=(10ⁿ-1)/9. 
Notice R_n divides R_m whenever n divides m.

Repunit primes are repunits that are prime.

 For example, 11, 1111111111111111111, and 11111111111111111111111 (2, 19, and 23 digits). The only other known repunit primes are the ones with 317 digits: (10³¹⁷-1)/9, 1,031 digits and (10¹⁰³¹-1)/9.

Factorization of decimal repunits

(Prime factors colored red means "new factors", i. e. the prime factor divides R_n but does not divide R_k for all k < n) (sequence A102380 in the OEIS)^[2]

R1 = 1 R2 = 11 R3 = 3 · 37 R4 = 11 · 101 R5 = 41 · 271 R6 = 3 · 7 · 11 · 13 · 37 R7 = 239 · 4649 R8 = 11 · 73 · 101 · 137 R9 = 32 · 37 · 333667 R10 = 11 · 41 · 271 · 9091

R11 = 21649 · 513239 R12 = 3 · 7 · 11 · 13 · 37 · 101 · 9901 R13 = 53 · 79 · 265371653 R14 = 11 · 239 · 4649 · 909091 R15 = 3 · 31 · 37 · 41 · 271 · 2906161 R16 = 11 · 17 · 73 · 101 · 137 · 5882353 R17 = 2071723 · 5363222357 R18 = 32 · 7 · 11 · 13 · 19 · 37 · 52579 · 333667 R19 = 1111111111111111111 R20 = 11 · 41 · 101 · 271 · 3541 · 9091 · 27961

R21 = 3 · 37 · 43 · 239 · 1933 · 4649 · 10838689 R22 = 112 · 23 · 4093 · 8779 · 21649 · 513239 R23 = 11111111111111111111111 R24 = 3 · 7 · 11 · 13 · 37 · 73 · 101 · 137 · 9901 · 99990001 R25 = 41 · 271 · 21401 · 25601 · 182521213001 R26 = 11 · 53 · 79 · 859 · 265371653 · 1058313049 R27 = 33 · 37 · 757 · 333667 · 440334654777631 R28 = 11 · 29 · 101 · 239 · 281 · 4649 · 909091 · 121499449 R29 = 3191 · 16763 · 43037 · 62003 · 77843839397 R30 = 3 · 7 · 11 · 13 · 31 · 37 · 41 · 211 · 241 · 271 · 2161 · 9091 · 2906161

Smallest prime factor of R_n for n > 1 are

11, 3, 11, 41, 3, 239, 11, 3, 11, 21649, 3, 53, 11, 3, 11, 2071723, 3, 1111111111111111111, 11, 3, 11, 11111111111111111111111, 3, 41, 11, 3, 11, 3191, 3, 2791, 11, 3, 11, 41, 3, 2028119, 11, 3, 11, 83, 3, 173, 11, 3, 11, 35121409, 3, 239, 11, ... (sequence A067063 in the OEIS)

la physique marche vers la vie ... au travers du chiffre et du nombre

source

On passe de A à B par * / + - ! , il y a une "durée" entre A et B, (A;durée;C)

 (A/B;B/A,A^B ...... etc.) arithmétique

A│B et B│A : fusion de A et B par l'opérateur │

10! secondes = A

6 semaines = B

10!  secondes = 6 semaines

e Nombre exponentiel ou nombre de Neper

e  = 2, 7182818284  5904523536  0287471352  6624977572  4709369995

   9574966967  6277240766  3035354759  4571382178  5251664274 …

    Notez que 2,7 est suivi de deux fois 1828.

Fraction continue

e = 2,718 …   =  [2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8...]

C'est Euler qui calcule la fraction continue de la base des logarithmes népériens et constate le développement périodique en 1, 2k, 1.

Cette périodicité prouve que e est irrationnel.

       e est l'initiale de exponentiel (nom donné par Euler) d'où le nom parfois donné à e: constante ou nombre d'Euler.

       e désigne la base du logarithme népérien (ou naturel).n

Nombres de Bernoulli

http://pi314.net/fr/bernoulli.php

Jacques Bernoulli connaissait quelques formules comme^[1],[2],[3] :
${\displaystyle {\begin{aligned}1+2+3+\cdots +(n-1)&={\frac {1}{2}}n^{2}-{\frac {n}{2}}&&={\frac {n(n-1)}{2}}\,;\\1^{2}+2^{2}+3^{2}+\cdots +{(n-1)}^{2}&={\frac {1}{3}}n^{3}-{\frac {1}{2}}n^{2}+{\frac {n}{6}}&&={\frac {n(n-1)(2n-1)}{6}}\,;\\1^{3}+2^{3}+3^{3}+\cdots +{(n-1)}^{3}&={\frac {1}{4}}n^{4}-{\frac {1}{2}}n^{3}+{\frac {1}{4}}n^{2}&&={\frac {n^{2}(n-1)^{2}}{4}}\,;\\1^{4}+2^{4}+3^{4}+\cdots +{(n-1)}^{4}&={\frac {1}{5}}n^{5}-{\frac {1}{2}}n^{4}+{\frac {1}{3}}n^{3}-{\frac {n}{30}}&&={\frac {n(n-1)(2n-1)(3n^{2}-3n-1)}{30}}\,;\\1^{5}+2^{5}+3^{5}+\cdots +{(n-1)}^{5}&={\frac {1}{6}}n^{6}-{\frac {1}{2}}n^{5}+{\frac {5}{12}}n^{4}-{\frac {1}{12}}n^{2}&&={n^{2}(n-1)^{2}(2n^{2}-2n-1) \over 12}.\end{aligned}}}$ Bernoulli observa que l'expression
${\displaystyle S_{m}(n)=\sum _{k=0}^{n-1}k^{m}=0^{m}+1^{m}+2^{m}+\cdots +{(n-1)}^{m}}$ est toujours un polynôme en n, de degré m + 1, de terme constant nul, dont le monôme dominant est ${\displaystyle {\frac {n^{m+1}}{m+1}}}$ et le monôme de degré m est^[4] (si m > 0) ${\displaystyle -{\dfrac {n^{m}}{2}}}$. On démontre (voir plus bas le paragraphe « Formules de récurrence ») que plus généralement, pour 0 ≤ k ≤ m, le coefficient de n^m+1–k est le produit par m!/(m + 1 – k)! d'un nombre qui dépend seulement de k et pas de m. On peut donc définir les nombres de Bernoulli B_k par :
${\displaystyle S_{m}(n)=\sum _{k=0}^{m}{\frac {m!}{(m+1-k)!}}{\frac {B_{k}}{k!}}\,n^{m+1-k}={1 \over {m+1}}\sum _{k=0}^{m}{m+1 \choose k}B_{k}\,n^{m+1-k}=\sum _{k=0}^{m}{m \choose k}B_{k}\,{\frac {n^{m+1-k}}{m+1-k}}.}$

ζ(2) :

la convergence vers p (n de 1000 en 1000) est assez lente : 3,14159... n'est atteint que pour n = 360 000.