PI et CKPLAN

PI et CKPLAN

Bienvenue

“The methods of theoretical physics should be applicable to all those branches of thought in which the essential features are expressible with numbers.”
—

Paul Dirac ((from the speech at the Nobel Banquet in Stockholm, December 10, 1933)


"l'univers est nombre."
"l'univers est écrit en langage mathématique. " Galilée
Le nombre porte en lui sa dimension temporelle ET matérielle.



R.G.U. : Réalité Générale de l'Univers



et

le temps .






Et Dieu créa le nombre, comme mesure du temps, l'homme le chiffre.

Constante arithmétique (Cf constante cosmologique) :
CKPLAN=5,55382562855700000E-17



"13 chiffres significatifs, somme 66 "











Me signaler par E-Mail , ou au tel , les inepties, ou erreurs ou imprécisions, banalités, ouverture de portes ouvertes, en faisant référence au message ECRIT ou vous n’êtes pas d'accord ou dans le doute, ou dans la compréhension , et non pas à des considérations philosophiques ou littéraires, générales .



CARPE DIEM.



Rendons grâce à Dieu.


Suivez les mises à jour en inscrivant votre e-mail :

jeudi 17 août 2017

Loi de Benford

http://fr.wikipedia.org/wiki/Loi_de_Benford



http://www.math-info.univ-paris5.fr/smel/articles/benford/cadre_benford.html

Resources

Calculateur en ligne de la loi de Benford
Fréquences relatives d’apparition de la 1ère décimale d’un résultat de mesure selon la Loi de Benford:


Loi de Benford -Fréquence relative


Loi de Benford et suites récurrentes

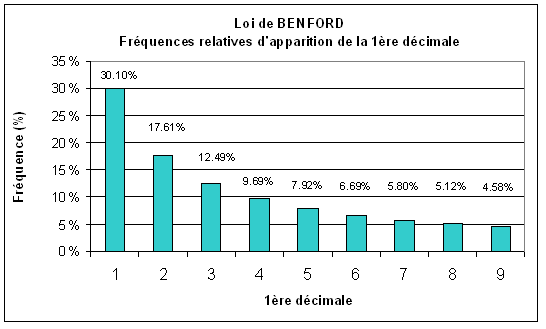
  La loi de Benford prévoit que dans les ensembles de nombres, ( prix des articles contenus dans un caddie, masses moléculaires des produits présentés dans un catalogue, population des agglomérations d'un pays...), le 1er chiffre (celui de gauche ) sera "1" dans 30.1% des cas, "2" dans 17.6% ... et "9" dans seulement 4.6%. Surprenant mais logique : statistiquement vérifiable et mathématiquement démontrable.
  Et avec les suites récurrentes ? Si pour la célèbre suite de Fibonacci l'accord est parfait, dans la suite un=4un-1 +3un-2 , avec u0=2 et u1=11, tous les nombres depuis u0 jusqu'à u200 (u200= 5.98..10 133) commencent par 1, 2 ou 5 avec une rigoureuse régularité, mais au-delà ?
Publié par le
Libellés : ,

Aucun commentaire:

Enregistrer un commentaire

Inscription à : Publier les commentaires (Atom)

Bases de numération

From: To:
Result:
UnitConversion.org - the ultimate unit conversion resource.