http://www.spiritart.org/Numbers/Pi/
base8: 3.1103755242...
http://forums.futura-sciences.com/mathematiques-superieur/296214-pi-base-8-a.html
http://mathworld.wolfram.com/PiDigits.html
In the following, the word "digit" refers to decimal digit after the decimal point. The following table gives the starting positions for strings of
| Sloane | positions | ||
| 0 | 1 | A037008 | 32, 50, 54, 65, 71, 77, 85, 97, ... |
| 0 | 2 | A050201 | 307, 360, 601, 602, 855, 856, 973, ... |
| 0 | 3 | A050202 | 601, 855, 1598, 4255, 4793, 7832, ... |
| 0 | 4 | A050203 | 13390, 17534, 17535, 37322, ... |
| 0 | 5 | A083599 | 17534, 211058, 215287, 652115, ... |
| 0 | 6 | A083600 | 1699927, 2328783, 2609392, ... |
| 0 | 7 | A083601 | 3794572, 13310436, 28970114, ... |
| 0 | 8 | 172330850, 184688988, ... |
| 1 | 1 | A037000 | 1, 3, 37, 40, 49, 68, 94, 95, ... |
| 1 | 2 | A050208 | 94, 153, 154, 174, 362, 395, 427, ... |
| 2 | 1 | A037001 | 6, 16, 21, 28, 33, 53, 63, 73, 76, ... |
| 2 | 2 | A050215 | 135, 185, 484, 535, 661, 687, 824, ... |
| 3 | 1 | A037002 | 9, 15, 17, 24, 25, 27, 43, 46, 64, ... |
| 3 | 2 | A050222 | 24, 215, 230, 282, 364, 401, 503, ... |
| 4 | 1 | A037003 | 2, 19, 23, 36, 57, 59, 60, 70, 87, ... |
| 4 | 2 | A050230 | 59, 125, 182, 201, 217, 453, 511, ... |
| 5 | 1 | A037004 | 4, 8, 10, 31, 48, 51, 61, 90, ... |
| 5 | 2 | A050238 | 130, 177, 178, 315, 809, 914, ... |
| 5 | 3 | A083620 | 177, 1232, 1450, 2359, 2674, 7245, .. |
| 6 | 1 | A037005 | 7, 20, 22, 41, 69, 72, 75, 82, ... |
| 6 | 2 | A050245 | 117, 211, 257, 276, 309, 377, 516, ... |
| 7 | 1 | A036974 | 13, 29, 39, 47, 56, 66, 96, 99, 120, ... |
| 7 | 2 | A050254 | 559, 621, 625, 633, 739, 742, 890, ... |
| 8 | 1 | A037006 | 11, 18, 26, 34, 35, 52, 67, 74, 78, ... |
| 8 | 2 | A050263 | 34, 204, 317, 322, 372, 472, 848, ... |
| 9 | 1 | A037007 | 5, 12, 14, 30, 38, 42, 44, 45, 55, ... |
| 9 | 2 | A050272 | 44, 79, 459, 705, 747, 762, 763, ... |
| 9 | 3 | A083642 | 762, 763, 764, 765, 2949, 7759, ... |
| 9 | 4 | A083643 | 762, 763, 764, 17988, 19437, 19446, ... |
| 9 | 5 | A083644 | 762, 763, 19446, 56988, 161862, ... |
| 9 | 6 | A083645 | 762, 193034, 1722776, 1722777, ... |
The following table gives the first few positions at which a digit 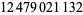 occurs
occurs 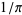 times. The sequence 1, 135, 1698, 54525, 24466, 252499, 3346228, 46663520, ... (Sloane's A061073) given by the diagonal is known as the Earls sequence (Pickover 2002, p. 339). Note that the sequence 9999998 occurs at decimal 762 (which is sometimes called the Feynman point; Wells 1986, p. 51). This is the largest value of any seven digits in the first million decimals.
times. The sequence 1, 135, 1698, 54525, 24466, 252499, 3346228, 46663520, ... (Sloane's A061073) given by the diagonal is known as the Earls sequence (Pickover 2002, p. 339). Note that the sequence 9999998 occurs at decimal 762 (which is sometimes called the Feynman point; Wells 1986, p. 51). This is the largest value of any seven digits in the first million decimals.
| Sloane | strings of 1, 2, ... | |
| 0 | A050279 | 32, 307, 601, 13390, 17534, 1699927, ... |
| 1 | A035117 | 1, 94, 153, 12700, 32788, 255945, ... |
| 2 | A050281 | 6, 135, 1735, 4902, 65260, 963024, ... |
| 3 | A050282 | 9, 24, 1698, 28467, 28467, 710100, ... |
| 4 | A050283 | 2, 59, 2707, 54525, 808650, 828499, ... |
| 5 | A050284 | 4, 130, 177, 24466, 24466, 244453, ... |
| 6 | A050285 | 7, 117, 2440, 21880, 48439, 252499, ... |
| 7 | A050286 | 13, 559, 1589, 1589, 162248, 399579, ... |
| 8 | A050287 | 11, 34, 4751, 4751, 213245, 222299, ... |
| 9 | A048940 | 5, 44, 762, 762, 762, 762, 1722776, ... |
The beast number 666 appears in 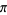 at decimals 2440, 3151, 4000, 4435, 5403, 6840, (Sloane's A083625). The first occurrences of just
at decimals 2440, 3151, 4000, 4435, 5403, 6840, (Sloane's A083625). The first occurrences of just 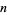 consecutive 6s are 7, 117, 2440, 21880, 48439, 252499, 8209165, 55616210, 45681781, ... (Sloane's A096760), while
consecutive 6s are 7, 117, 2440, 21880, 48439, 252499, 8209165, 55616210, 45681781, ... (Sloane's A096760), while 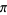 (or more) consecutive 6s first occur at 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (Sloane's A050285).
(or more) consecutive 6s first occur at 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (Sloane's A050285).
La somme des 144 premières décimales est égale à 666 ......
La somme des 20 premières décimales est égale à 100 ...
La somme des 200 premières décimales est égale à 900 ....
http://www.kristos.online.fr/pi3.14.htm
La somme des 144 premières décimales est égale à 666 ......
La somme des 20 premières décimales est égale à 100 ...
La somme des 200 premières décimales est égale à 900 ....
http://www.kristos.online.fr/pi3.14.htm




Aucun commentaire:
Enregistrer un commentaire