Eternité

Représentée par :
cardinal à un :
0
1
cardinal à deux :
00
11

cardinal à n :

(En) = .....000000000000000000......

Les zéros sont un comptage d'un temps.

card ((En))

ou par :

(E'n) = .....11111111111111111111......

Les 1 sont un comptage  de temps .

card ((E'n))

autre représentation :

.....000000000000010000000000000....


ou encore :
.....1111111111111101111111111111......

ces motifs de 1 ou/et 0 sont du type (2^n) ou et (2^n)+1  et ou (2^n) -1 ...

avec 2^0=1 par convention.

Cela traduit trois états.
avant, pendant, après.

Il est clair qu'il faut deux changement d'états pour espérer revenir à une situation initiale ...

000000100000001000000
ou
11111011111111111111111111101111111111


cela donne cinq dimensions ....

01010 soit 10 en base 10  avec 16=2^5
10101 soit 21 en base 10

Multiplication par 2 en base 2 , par 10 en base 10

http://fr.wikipedia.org/wiki/Syst%C3%A8me_binaire#Code_de_Gray_ou_binaire_r.C3.A9fl.C3.A9chi

Une multiplication par 2 en base 2 , avec les symboles initiaux 0 et 1 , revient avec nos conventions d'écriture à ajouter un zéro à droite.
0
1
0 > 00 lire 0 devient 00 dans le temps supposé s'écouler de la gauche vers la droite
1 > 10
00 > 000
10 > 100
000 > 0000
100 > 1000
0000 > 00000
1000 > 10000
etc .

On peut faire une lecture en base 10 des résultats.
0
1
00 : ??
10 : 2
000 : ??
100 : 4
0000 ??
1000 : 8
00000 ???
10000 : 16
000000 : ??
100000 : 32

En base 10 une multiplication par 10 revient à ajouter un zéro à droite avec nos dix "symboles initiaux" (0123456789)
00   ????
10
20
30
40
50
60
70
80
90

On peut en faire une écriture , chiffre par chiffre en base 2, puis une traduction en base 10
00 > 00
10 > 10 : 2
20 > 100 : 4
30  > 110 : 6
40 > 1000 : 8
50 > 1010 : 10
60  > 1100 : 12
70 >  1110 : 14
80 >  10000 16
90 >  10010 : 18
100 > 1000 : 8
200 > 1000 : 16
300 > 1100 : 12
400 > 10000 : 16
500 > 10100 : 20
600 > 11000 : 24
700 > 11100 : 28
800 > 100000 : 32
900 > 100100 : 36
1000 > 10000 : 16
2000 > 100000 : 32
3000 > 110000 : 48
4000 > 1000000 : 64
5000 > 1010000 : 80
6000 > 1100000 : 96
7000 > 1110000 : 112
8000 > 10000000 : 128
9000 > 10010000 : 144
etc.

La aussi la multiplication par 10 en base 10 traduit une stabilité du contenu dans le temps.

Egalité quantique en base 10 , ajout de temps, même contenu  :

154 == 1540 === 15400 etc .....


Egalité quantique en base 2, ajout de temps, même contenu :

1110 == 11100

Il y a deux familles en base 2 , 0 et 1.









Ce qui traduit un avancement dans le temps ....

Symétrie T

http://fr.wikipedia.org/wiki/Sym%C3%A9trie_T

renversement du temps

00
11



000
101
010
111

0000
1111
1001
0110

etc ..


Palindrome sur les chiffres constituant un nombre ( partie entière et/ou partie décimale sur R).

Théorème du viriel

http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_du_viriel


http://florenaud.free.fr/Viriel.php

Lecture et compréhension du chiffre nombre en base 2 et base 10

En base 2 ,
on a le déroulement d'un temps ET d'un contenu
10001000101110110011011111111 ....

gauche vers droite ou/ET droite vers gauche

00000000000000000000000
111111111111111111111........  (2^n)-1 1 3 7 15 31 63 127 255 511 1023

Il faut introduire la "virgule binaire"

1110000100000111,0010000110

pou avoir deux états distincts : onde et matière

écrire 1001 base 2

peut se lire

9 en base 10
1,001 en base 2
1,4 en base 10  , lecture palindrome ( renversement du temps) 001>>>100 = 4

10,01 en base 2
2,2 en base 10

100,1 en base 2
4,1 lecture gauche droite en base 10

PI bases de numération

http://www.spiritart.org/Numbers/Pi/

base₈: 3.1103755242...


http://forums.futura-sciences.com/mathematiques-superieur/296214-pi-base-8-a.html

http://mathworld.wolfram.com/PiDigits.html

In the following, the word "digit" refers to decimal digit after the decimal point. The following table gives the starting positions for strings of  copies of the digit  in the first  digits of .

		Sloane	positions
0	1	A037008	32, 50, 54, 65, 71, 77, 85, 97, ...
0	2	A050201	307, 360, 601, 602, 855, 856, 973, ...
0	3	A050202	601, 855, 1598, 4255, 4793, 7832, ...
0	4	A050203	13390, 17534, 17535, 37322, ...
0	5	A083599	17534, 211058, 215287, 652115, ...
0	6	A083600	1699927, 2328783, 2609392, ...
0	7	A083601	3794572, 13310436, 28970114, ...
0	8		172330850, 184688988, ...

1	1	A037000	1, 3, 37, 40, 49, 68, 94, 95, ...
1	2	A050208	94, 153, 154, 174, 362, 395, 427, ...

2	1	A037001	6, 16, 21, 28, 33, 53, 63, 73, 76, ...
2	2	A050215	135, 185, 484, 535, 661, 687, 824, ...

3	1	A037002	9, 15, 17, 24, 25, 27, 43, 46, 64, ...
3	2	A050222	24, 215, 230, 282, 364, 401, 503, ...

4	1	A037003	2, 19, 23, 36, 57, 59, 60, 70, 87, ...
4	2	A050230	59, 125, 182, 201, 217, 453, 511, ...

5	1	A037004	4, 8, 10, 31, 48, 51, 61, 90, ...
5	2	A050238	130, 177, 178, 315, 809, 914, ...
5	3	A083620	177, 1232, 1450, 2359, 2674, 7245, ..

6	1	A037005	7, 20, 22, 41, 69, 72, 75, 82, ...
6	2	A050245	117, 211, 257, 276, 309, 377, 516, ...

7	1	A036974	13, 29, 39, 47, 56, 66, 96, 99, 120, ...
7	2	A050254	559, 621, 625, 633, 739, 742, 890, ...

8	1	A037006	11, 18, 26, 34, 35, 52, 67, 74, 78, ...
8	2	A050263	34, 204, 317, 322, 372, 472, 848, ...

9	1	A037007	5, 12, 14, 30, 38, 42, 44, 45, 55, ...
9	2	A050272	44, 79, 459, 705, 747, 762, 763, ...
9	3	A083642	762, 763, 764, 765, 2949, 7759, ...
9	4	A083643	762, 763, 764, 17988, 19437, 19446, ...
9	5	A083644	762, 763, 19446, 56988, 161862, ...
9	6	A083645	762, 193034, 1722776, 1722777, ...

The following table gives the first few positions at which a digit 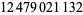 occurs  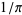times. The sequence 1, 135, 1698, 54525, 24466, 252499, 3346228, 46663520, ... (Sloane's A061073) given by the diagonal is known as the Earls sequence (Pickover 2002, p. 339). Note that the sequence 9999998 occurs at decimal 762 (which is sometimes called the Feynman point; Wells 1986, p. 51). This is the largest value of any seven digits in the first million decimals.

	Sloane	strings of 1, 2, ...s first occur at
0	A050279	32, 307, 601, 13390, 17534, 1699927, ...
1	A035117	1, 94, 153, 12700, 32788, 255945, ...
2	A050281	6, 135, 1735, 4902, 65260, 963024, ...
3	A050282	9, 24, 1698, 28467, 28467, 710100, ...
4	A050283	2, 59, 2707, 54525, 808650, 828499, ...
5	A050284	4, 130, 177, 24466, 24466, 244453, ...
6	A050285	7, 117, 2440, 21880, 48439, 252499, ...
7	A050286	13, 559, 1589, 1589, 162248, 399579, ...
8	A050287	11, 34, 4751, 4751, 213245, 222299, ...
9	A048940	5, 44, 762, 762, 762, 762, 1722776, ...

The beast number 666 appears in 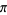 at decimals 2440, 3151, 4000, 4435, 5403, 6840, (Sloane's A083625). The first occurrences of just  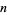consecutive 6s are 7, 117, 2440, 21880, 48439, 252499, 8209165, 55616210, 45681781, ... (Sloane's A096760), while  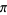(or more) consecutive 6s first occur at 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (Sloane's A050285).


La somme des 144 premières décimales est égale à 666 ......
La somme des 20 premières décimales est égale à 100 ...
La somme des 200 premières décimales est égale à 900 ....


http://www.kristos.online.fr/pi3.14.htm