Nombre pentagonal
En mathématiques, un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Pour tout entier n ≥ 1, d'après les formules générales pour les nombres polygonaux, le n-ième nombre pentagonal est donc la somme des n premiers termes de la suite arithmétique de premier terme 1 et de raison 31 :
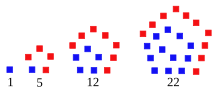
soit le tiers du (3n – 1)-ième nombre triangulaire et les dix premiers sont 1, 5, 12, 22, 35, 51, 70, 92, 117 et 145 (suite A000326 de l'OEIS).
Les nombres pentagonaux sont importants dans la théorie des partitions d'entiers d'Euler et interviennent par exemple dans son théorème des nombres pentagonaux.
Test des nombres pentagonaux[modifier | modifier le code]
Un réel positif x est pentagonal si et seulement si l'équation du second degré 3n2 – n – 2x possède une solution entière n > 0, c'est-à-dire si le réel suivant est entier :
Lorsque n est entier, x est le n-ième nombre pentagonal.
Nombres pentagonaux généralisés[modifier | modifier le code]
Les nombres pentagonaux généralisés sont les nombres de la forme n(3n – 1)/2, mais avec n entier relatif, ou encore : les nombres de la forme n(3n ± 1)/2 avec n entier naturel. Les vingt premiers termes de cette suite d'entiers sont 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126 et 145 (suite A001318 de l'OEIS).






Aucun commentaire:
Enregistrer un commentaire