http://fr.wikipedia.org/wiki/Co%C3%AFncidence_math%C3%A9matique
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Nb163.htm
Sur les nombres "quasi-entiers" , presque entiers
x,999999...999y
z,0000000000 .... 000t
Prenons le nombre pi, l'exponentielle, la racine carrée et le nombre premier 163, et mélangeons le tout. En mélangeant tout ça, on devrait a priori obtenir un nombre complètement banal... Et pourtant, quand on effectue le calcul, on tombe sur
eπ.√163 = 262537412640768743, 9999999999992...
Ce nombre, parfaitement irrationnel, est presque un entier ! A 10-12 près, c'est quand même pas mal (si on avait voulu le faire exprès, on aurait pas réussi). La découverte de ce phénomène est attribuée à Alexandre Aitken, et on est aujourd'hui incapable d'expliquer d'où ça vient ! En changeant 163 par d'autres nombres entiers, on trouve relativement souvent des nombres presque entiers, ce qui prête à penser qu'il y a là un authentique mystère à étudier.
Quelques éléments de réponse tout de même : s'il y a bien un mystère, il sera difficile à étudier ! On peut voir qu'elle a des liens avec la fonction modulaire j (celle du monstrous moonshine)... Avec cette observation, on a pu fabriquer de très jolis nombres presque entiers, comme :
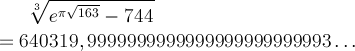
Voir CKPLAN*(2^66)




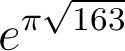

Aucun commentaire:
Enregistrer un commentaire