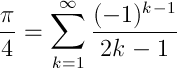
La série de Leibniz, et on le sait depuis Leibniz, est une série infinie qui converge vers π/4. La série est infinie, mais si on ne prend qu'un nombre fini de termes, on peut théoriquement obtenir une approximation de pi. Dans la pratique, on n'utilise jamais cette série pour approximer pi, la convergence est bien trop mauvaise (après n termes, l'erreur est de l'ordre de 1/n). Ainsi, si on fait la somme en prenant les 50 000 premiers termes, on obtient seulement 4 décimales correctes :
3.1415726535897952384626423832795041041971666293751
La valeur exacte de pi étant :
3.1415926535897932384626433832795028841971693993751
Fait particulièrement étrange :
les premières décimales de la valeur approchée
de pi sont toutes correctes,
à quelques décimales près !
Pourquoi cette étrangeté ?
Personne ne le sait !
les premières décimales de la valeur approchée
de pi sont toutes correctes,
à quelques décimales près !
Pourquoi cette étrangeté ?
Personne ne le sait !
En fait, si, on le sait. Le phénomène, observé pour la première fois en 1982, s'explique grâce aux formules d'Euler-Mc Laurin. Dans les bons cas (N multiple de 4), on a le développement asymptotique suivant :

Autrement dit, quand N est une grande puissance de 10, les décimales fausses de développement décimal seront isolées. Notons au passage que le phénomène est moins présent quand on prend les 50001 premières décimales :
3.1416126531897992384226427832755041441967666333751
recherche dans pi :
360 en position 285 et 358 1412 1828 3296 3753 4081 4721 5383 5421 8658 8984 9280 9652 9735 etc ....
001 en 360 et 973 1608 2339 5168 9898 9906 9984 etc .....
Dites-moi un truc marrant sur les décimales de pi...
Parce que les décimales de pi, à partir de la 242422e décimale, sont 42424242...
Parce que les décimales de pi, à partir de la 242422e décimale, sont 42424242...
Et je crois que j'oublie d'autres détails absolument importants,
comme le fait que 666×667=444222 ;
que 42 est la somme de deux nombres premiers consécutifs (42=19+23) ;
que la plus petite façon d'écrire 1 en une somme de 4 fractions différentes est 1=1/2 + 1/3 + 1/7 + 1/42 ;
que le nombre 10 peut s'écrire comme somme d'entiers non nuls de 42 façons différentes ;
qu'un nombre de la forme n7-n est toujours divisible par 42 .......

Euler
sur ce site :
http://www.pi314.net/fr/leibniz.php
On lit :
"
Si il y a quelques décimales en marron, c'est parce qu'elles sont fausses! Mais alors, pourquoi les suivantes sont-elles justes? Car enfin la convergence est bien logarithmique d'après la forme (environ log(n)) ! C'est le problème que Roy North a posé aux frères Borwein il y a quelques années... Je n'ai plus la solution, mais elle fait intervenir les nombres d'Euler et deux formules de sommation. En attendant des recherches ultérieures...







Aucun commentaire:
Enregistrer un commentaire