Trois manières d'exprimer des durées , surfaces ( KEPLER).
D1 = D2 + D3
Il existe une longueur minimum pour AC ......
Cf triplets pythagoriciens ...
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_deux_lunules
La conjecture de Syracuse est une autre manière d'exprimer des durées, avec deux familles ....
Il ne faut pas parler de pairs et d'impairs pour les nombres entiers , mais faire une autre partition de N .
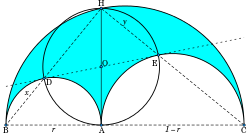
Arbelos ; Pore du savetier
N° 2 : La conjecture de Syracuse
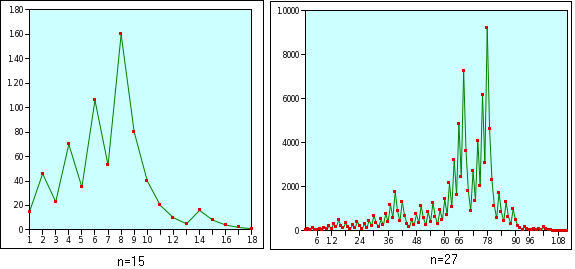
Prenez un entier supérieur à 1. S'il est pair, divisez le par 2, et s'il est impair, multipliez-le par 3 et ajoutez 1. Réitérez ensuite les deux précédentes étapes. Quel que soit l'entier n choisi au départ, la suite finira par retomber à 1... Et personne ne sait pourquoi ! C'est la célèbre conjecture de Syracuse, d'apparence très simple, mais finalement insaisissable.
Quel rapport avec la ville sicilienne ? Eh bien, absolument aucun ! En fait, le problème a connu son heure de gloire dans les années 50, quand Helmut Hasse a fait une conférence sur le sujet à l'université de Syracuse... à New York !
source :
http://eljjdx.canalblog.com/tag/Conjectures
calcul syracuse :
http://calculis.net/syracuse
Pour 5 :
calcul syracuse :
http://calculis.net/syracuse
Pour 5 :
5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 5 est de 5 et son altitude est de 16.
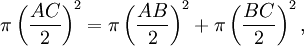
Aucun commentaire:
Enregistrer un commentaire