Théorème des 4 carrés

24642


https://fr.m.wikipedia.org/wiki/Théorème_des_quatre_carrés_de_Lagrange

Loi de la gravitation

la loi de l'attraction universelle, encore nommée loi de la gravitation. 
Newton dit que deux corps massifs A et B de masse m_A et m_B, distants de r mètres, 
exercent l'un sur l'autre une force égale à 

FA/B=FB/A=GmAmBr2${\mathrm{<br>}}_{}$

avec G une constante, dite "constante de gravitation universelle" égale à 6.67*10^-11 N.m².kg^-2. 

Dans les unités SI, le CODATA recommande la valeur suivante² :

${\displaystyle G=6{,}674\,08\times 10^{-11}\;{\mbox{N}}\cdot {\mbox{m}}^{2}\cdot \ {\mbox{kg}}^{-2}}$

avec une incertitude standard de

${\displaystyle \pm 0{,}000\,31\times 10^{-11}\;{\mbox{N}}\cdot {\mbox{m}}^{2}\cdot \ {\mbox{kg}}^{-2}.}$

https://fr.wikipedia.org/wiki/Loi_universelle_de_la_gravitation

DIVISIBILITE par 7

http://afrique.le360.ma/autres-pays/societe/2019/11/14/28555-royaume-uni-un-jeune-nigerian-decore-pour-avoir-trouve-une-nouvelle-formule-mathematique
Sept/six  jours pour la création du monde par Dieu. BIBLE.

moines cisterciens à la fin du XIIIe siècle

 

l'astucieux système de numérotation utilisé en Europe pendant des siècles... qui a ensuite été entièrement oublié

Développée par des moines cisterciens à la fin du XIIIe siècle, cette méthode d'écriture des chiffres a été utilisée dans les monastères de toute l'Europe pendant au moins deux siècles.

À l'époque, les chiffres arabes gagnaient du terrain sur la version romaine, mais il faudra des siècles avant que le nouveau système ne soit largement accepté.

Les Cisterciens ne semblaient pas peser d'un côté ou de l'autre sur ce différend : leur notation était plutôt une troisième alternative, utile aux moines européens, de l'Angleterre à l'Italie, de l'Espagne à la Suède.

Et elle jouissait d'une certaine popularité car, contrairement aux chiffres romains, elle offrait la possibilité de représenter n'importe quel nombre par un seul symbole.

Légende image,

Ces numéros ont quatre chiffres en notation arabe et 1 993 nécessite huit chiffres romains : MCMXCII

Cependant, comme le système romain, le cistercien ne se prêtait pas facilement à la multiplication ou à la division.

Au moment où le livre imprimé a remplacé le manuscrit comme moyen de transmission du savoir, 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9 avaient déjà conquis le monde.

Les Romains I, V, X, L, C, D et M avaient leur place réservée pour la postérité.

Lire aussi :

• La bibliothèque islamique où les mathématiques modernes ont émergé
• La femme qui a changé les mathématiques
• Comment les mathématiques ont aidé à construire la Chine impériale

Mais les chiffres cisterciens ont été écartés à tel point qu'un siècle plus tard, ils étaient devenus un mystère.

Une exception, note King, est l'utilisation de la notation jusqu'au XVIIIe siècle pour marquer les volumes sur les barriques de vin et les balances à jauge en Flandre.

CRÉDIT PHOTO,BODLEIAN LIBRARY. OXFORD UNIVERSITY

Légende image,

Une illustration de la vinification qui apparaît dans un manuscrit flamand du 14ème siècle

Les chiffres cisterciens n'ont refait surface que quelques fois dans l'histoire, notamment après avoir été adoptés par les francs-maçons à Paris en 1780, et dans les écrits nationalistes du XXe siècle sur le folklore allemand.

Mais comment ce système - décrit comme "des chiffres très élégants" par le mathématicien allemand Agrippa de Nettesheim, de la Renaissance - a-t-il fonctionné ?

'Chiffres très élégants'

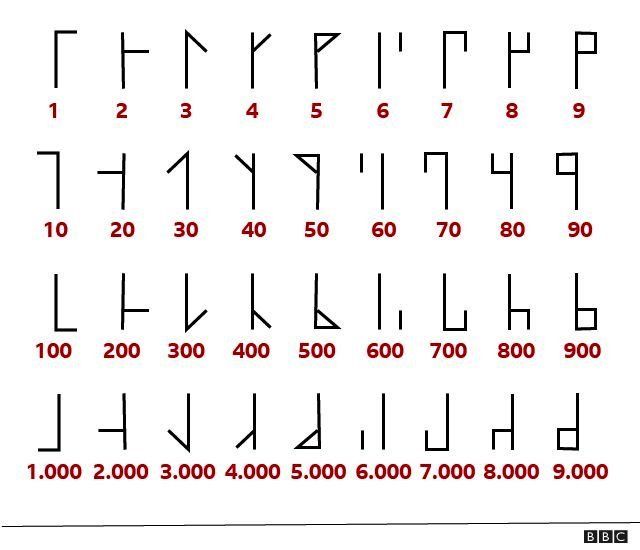
Selon King, le système des moines cisterciens était basé sur une simple notation pour représenter les nombres de 1 à 99 qui a été apportée en Angleterre depuis Athènes par le moine Jean de Basingstoke au début du 13ème siècle.

Au fil du temps, ce système a été étendu pour représenter n'importe quel nombre de 1 à 9 999 en un seul chiffre.

Lire aussi :

• 'Il faut changer la réputation des mathématiques'
• Pourquoi les mathématiques sont si complexes
• Cette théorie mathématique prétend que le voyage dans le temps est possible

Dans sa célèbre Chronica Majora, le moine bénédictin et historien Mateo de Paris enseigne comment les écrire.

Dans la figure ci-dessous, chaque coin, ou quadrant, contient une représentation des milliers (1), des centaines (2), des dizaines (3) et des unités (4), dans l'ordre suivant :

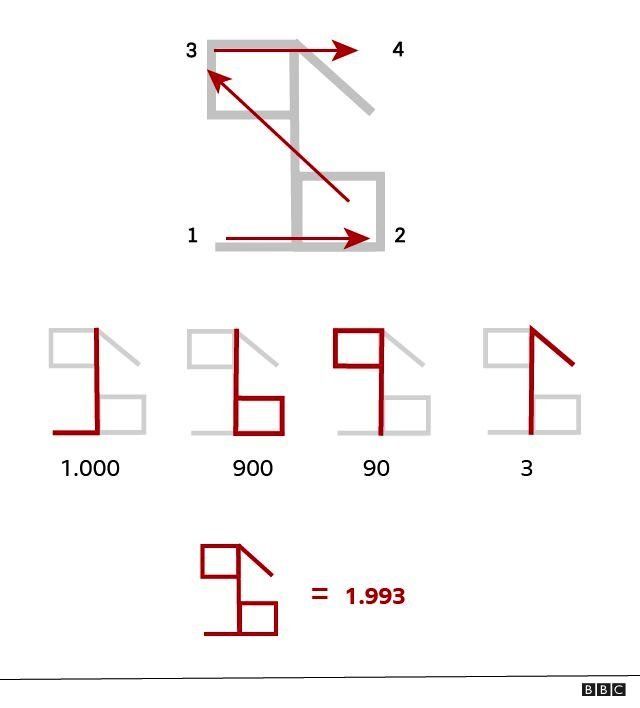
Au fur et à mesure de sa diffusion dans les monastères cisterciens, le système a subi de légères modifications en fonction de la langue parlée par les moines.

À un moment donné, la ligne initiale était horizontale, mais au 14e siècle, les moines français avaient remis cette tige dans sa position initiale.

Mateo de Paris a souligné que "ce qui est le plus admirable et ce que nous ne trouvons pas dans le cas des chiffres romains ou arabes est que tout nombre peut être représenté par un seul chiffre".

Le problème, bien sûr, est de savoir comment lire et écrire en utilisant le système. Mais si l'on suit les règles de base, ce n'est peut-être pas aussi difficile qu'il n'y paraît à première vue.