Source
Dans l'ordre implicite (ou implié), l'espace et le temps ne sont plus les facteurs dominants qui déterminent les relations de dépendance ou d'indépendance entre les éléments.
Un type entièrement différent de connexions fondamentales est possible, dont nos notions ordinaires de temps et d'espace, ainsi que celles relatives à des particules existant séparément, deviennent des abstractions de formes dérivées d'un ordre plus profond.
Ces notions ordinaires apparaissent dans ce qui est appelé l'ordre explicite (ou déplié), qui est une forme spéciale et distincte contenue dans la totalité générale de tous les ordres implicites / impliés
Wikipedia
PI et CKPLAN


Bienvenue
“The methods of theoretical physics should be applicable to all those branches of thought in which the essential features are expressible with numbers.”
| — | Paul Dirac ((from the speech at the Nobel Banquet in Stockholm, December 10, 1933) |
"l'univers est nombre."
"l'univers est écrit en langage mathématique. " Galilée
Suivez les mises à jour en inscrivant votre e-mail :
Le nombre porte en lui sa dimension temporelle ET matérielle.
R.G.U. : Réalité Générale de l'Univers
et
le temps .
Et Dieu créa le nombre, comme mesure du temps, l'homme le chiffre.
Constante arithmétique (Cf constante cosmologique) :
CKPLAN=5,55382562855700000E-17
"13 chiffres significatifs, somme 66 "
Me signaler par E-Mail , ou au tel , les inepties, ou erreurs ou imprécisions, banalités, ouverture de portes ouvertes, en faisant référence au message ECRIT ou vous n’êtes pas d'accord ou dans le doute, ou dans la compréhension , et non pas à des considérations philosophiques ou littéraires, générales .
CARPE DIEM.
Rendons grâce à Dieu.
Suivez les mises à jour en inscrivant votre e-mail :
mercredi 24 janvier 2018
dimanche 14 janvier 2018
Inverse premiers
CARRÉS MAGIQUES avec les décimales
de l'inverse des nombres PREMIERS

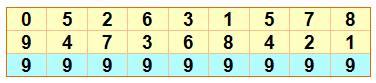
Notez toujours que chaque
moitié est le complément à 9 de l'autre:
 |
|
Bilan
Le carré avec 1/19 est
bien magique, mais c'est un des rares connus en base
10. Ils sont très nombreux en diversifiant la base.
Par exemple 1 / 53 en
base 12.
Ou encore 1 / 223 = 1
/ 220213 = 0,0000100210210102121211101202221112202… dont la somme
est 222.
|
jeudi 4 janvier 2018
Deux , la pensée, la parole,l'écrit et le nombre
«Monarque absolu» de notre logique binaire, il est aussi celui de l’accouplement avec lequel commence la société. Avec lui, vient l’autre. Méditation pour un 2 janvier.
- Ce que le «2» dit de nous
La fête de l’épiphanie, qui commémore la venue du Messie venu et incarné dans le monde, a lieu le 6 janvier, c’est les Rois, tout le monde sait cela. On sait moins que, depuis 1802, année de la naissance de Victor Hugo, mais les deux événements sont indépendants, cette célébration peut se tenir le premier dimanche qui suit le 1er janvier, selon un décret du cardinal Caprara, légat du pape Pie VII. Ainsi, le «2 janvier», le jour d’après, est tout de même premier en quelque chose : c’est le premier jour possible pour la fête des Rois. C’est arrivé en 2011. Hasard de la numérologie, cela se produira de nouveau en… 2022.
En mathématiques, le nombre 2 est chargé de significations et lourd de promesses. Pour un mathématicien, 2 est d’abord le premier (si, si) des nombres premiers. Vous savez ces nombres entiers qui ne sont divisibles par aucun nombre plus petit (sauf le 1). Euclide a montré, il y a deux mille cinq cents ans, qu’ils sont une infinité. L’une des raisons de la fascination pour les nombres premiers est que tout nombre entier est représentable d’une manière unique comme produit de nombres premiers. Ainsi, 12 = 2 × 2 × 3, 2018 = 2 × 1009, et mis à part l’ordre des facteurs, ces décompositions sont intangibles. C’est la raison pour laquelle le nombre 1 a été exclu de la liste : multipliez par 1 autant de fois que vous voudrez, vous ne changerez pas le résultat. C’est la version multiplicative de la tête à Toto.
Ainsi, 2 est premier, ce qui n’est pas son moindre titre de gloire, et c’est même le seul nombre premier pair, ce qui le met souvent à l’écart, mais il paraît qu’il ne s’en offusque pas, dans beaucoup de démonstrations mathématiques.
Le nombre 2 a aussi ses victimes. Le fameux théorème de Pythagore doit son nom au philosophe de Samos qui l’a énoncé au VIe siècle avant notre ère, mais il était connu des Mésopotamiens plus de mille ans auparavant. Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Considérons le carré de côté 1. Cet énoncé stipule donc que le carré de la diagonale est égal à 2. Selon une légende vraisemblable, Hippase de Métaponte, un pythagoricien, aurait découvert que cette diagonale ne peut être mesurée avec la même règle que le côté, aussi rapprochées que soient les graduations. Cela ne vous choque peut-être pas outre mesure (c’est l’expression qui convient) mais cette découverte mettait à mal l’entière conception du monde en vigueur dans cette école de pensée : «Toute chose est nombre.» Si le monde était censé être entièrement explicable par les nombres, comment pouvait-on concevoir que cette simple diagonale soit réfractaire à toute mesure raisonnable, c’est-à-dire rationnelle comme l’on dit aujourd’hui ? Porteur de cette terrible nouvelle, le pauvre Hippase aurait été jeté par-dessus bord ou sauvagement poignardé par ses condisciples. Ainsi, le nombre 2, pour innocent qu’il paraisse, aurait engendré le premier martyr de la science.
La résonance du 2, dans le monde des mathématiques, est infinie. L’un des concepts essentiels dans le développement de cette science, et particulièrement à notre époque, est celui de «dualité». Il s’agit là du deux du miroir, de celui de la symétrie, mais décliné et approfondi par des siècles de réflexion. L’évolution des mathématiques nous a progressivement amenés de l’étude des objets et des notions conçues pour modéliser le réel, vers l’étude des relations entre ces objets. Compter, c’est d’abord énumérer, donc additionner, mais la tentation est grande de pouvoir revenir sur ses pas : on définit alors l’opération duale qui est la soustraction. Sous une forme très générale, on peut dire que la dualité est, en substance, une opération de traduction de concepts, relations ou structures vers d’autres concepts, relations ou structures, effectuée d’une manière «biunivoque» : à chaque élément d’un monde correspond un et un seul élément de l’autre monde. Le plus souvent cette liaison est d’ailleurs subtilement réversible : si, à partir d’un objet A, on a obtenu un objet (dual) B, et que l’on réitère l’opération sur B, on retrouve A. Prendre le dual du dual, vous ramène au point de départ. Ouf.
Le miracle de la dualité est que cette exploitation de la symétrie enrichit considérablement le champ d’étude initial et permet des avancées spectaculaires. Si un système physique, comme une machine ou même un être vivant, évolue uniquement en fonction de son passé immédiat (disons son état dans la seconde précédente), l’étude mathématique pourra se fonder sur un modèle abstrait où un système évolue en fonction de son futur immédiat, autrement dit, l’état dans lequel il sera dans la seconde suivante. Ce modèle imaginaire, dual théorique sans assise physique du système réel, permettra cependant de décrire et de prévoir l’évolution effective du système considéré.
Le nombre 2 est aussi le «monarque absolu» de notre logique, dite du «tiers exclu» : une assertion est «juste» ou «fausse», une réponse est «oui» ou «non», le «courant passe» ou «ne passe pas». D’où son utilisation systématique en informatique, fondée sur une logique dite «binaire» : à partir de circuits électroniques susceptibles de prendre deux états, on peut mettre le monde en équations, transmettre et recueillir des informations, induire des évolutions, et,finalement, jouer à Dieu. Les ordinateurs quantiques du futur opéreront selon une logique comportant un nombre arbitraire, voire infini, d’états. Ce sera alors la première défaite du nombre 2. Mais nous n’en sommes pas là, et la logique binaire, pourtant si sommaire et restrictive, a encore de beaux jours devant elle. Ce n’est qu’avec une certaine réticence que les applications des mathématiques, et plus généralement les raisonnements humains, entrent dans l’univers inquiétant du peut-être.
L’histoire, qui ne s’arrête pas là, a peut-être débuté avec le nombre 2 qui est évidemment notre premier modèle du couple, qu’il soit homogène ou hétérogène, fondé sur la ressemblance ou sur le contraste. Et le couple est d’abord le lieu de la conversation et de la négociation puisqu’il ne peut contenir de majorité. Si deux ne sont pas d’accord, il faut parler. Ainsi, le nombre 2, à partir duquel commence la société, nous suggère, pour vivre ensemble, une voie fondée sur l’accord plus que sur la contrainte. Il contient en germe la notion de partage : 2 est par nature généreux.
De là à imaginer, en ce 2 janvier, que ce jour d’après soit aussi un jour d’attention et de sollicitude envers tous ceux qui frappent à notre porte parce qu’ils fuient la persécution ou la misère, il n’y a qu’un pas. Si le premier est le jour des vœux, pourquoi ne pas faire du deuxième jour de l’année le jour d’eux ? Car eux sont nous, c’est l’évidence.
Gérald Tenenbaum mathématicien, spécialiste de la théorie des nombres, et professeur à l’InstitutEn français
0 – zéro, 1 – un, 2 – deux, 3 – trois, 4 – quatre, 5 – cinq, 6 – six, 7 – sept, 8 – huit, 9 – neuf, 10 – dix
En anglais
0 – zero, 1- one, 2 – two, 3 – three, 4 – four, 5 – five, 6 – six, 7 – seven, 8 – eight, 9 – nine, 10 – ten
En allemand
0 – null, 1 – eins, 2 – zwei, 3 – drei, 4 – vier, 5 – fünf, 6 – sechs, 7 – sieben, 8 – acht, 9 – neun, 10 – zehn
En espagnol
0 – cero, 1 – uno, 2 – dos, 3 – tres, 4 – cuatro, 5 – cinco, 6 – seis, 7 – siete, 8 – ocho, 9 – nueve, 10 – diez
En catalan
0 – zero, 1 – un, 2 – dos, 3 – tres, 4 – quatre, 5 – cinc, 6 – sis, 7 – set, 8 – vuit, 9 – nou, 10 – deu
En portugais
0 – zero, 1- um, 2 – dois, 3 – três, 4 – quatro, 5 – cinco, 6 – seis, 7 – sete, 8 – oito, 9 – nove, 10 – dez
En italien
0 – zero, 1- uno, 2 – due, 3 – tre, 4 – quatro, 5 – cinque, 6 – sei, 7 – sette, 8 – otto, 9 – nove, 10 – dieci
En suédois
0 – noll, 1 – ett, 2 – två, 3 – tre, 4 – fyra, 5 – fem, 6 – sex, 7 – sju, 8 – åtta, 9 – nio, 10 – tio
En néerlandais
0 – zero, 1 – één, 2 – twee, 3 – drie, 4 – vier, 5 – vijf, 6 – zes, 7 – zeven, 8 – acht, 9 – negen, 10 – tien
En danois
0 – nul, 1 – en, 2 – to, 3 – tre, 4 – fire, 5 – fem, 6 – seks, 7 – syv, 8 – otte, 9 – ni, 10 – ti
En islandais
0 – núll, 1 – einn (m) / ein (w) / eitt (s), 2 – tveir (m) / tvær (w) / tvö (s), 3 – þrír (m) / þrjár (w) / þrjú (s), 4 – fjórir (m) / fjórar (w) / fjögur (s), 5 – fimm, 6 – sex, 7 – sjö, 8 – átta, 9 – níu, 10 – tíu
En polonais
0 – zero, 1 – jeden, 2 – dwa, 3 – trzy, 4 – cztery, 5 – pięć, 6 – sześć, 7 – siedem, 8 – osiem, 9 – dziewięć, 10 – dziesięć
En russe
0 - нулЬ [nol], 1 - один/раз [adin/ras], 2 - два [dva], 3 - три [tri], 4 - четыре [tchetyre], 5 - пять [piatt], 6 - шесть [chest], 7 - семь [siem], 8 - восемь [vosiem], 9 - девять [dieviats], 10 - десять [dieciats]
Inscription à :
Commentaires (Atom)
Bases de numération
UnitConversion.org - the ultimate unit conversion resource.

